Estimating fixed-point range and resolution
An example of selecting a fixed-point format based on the context.
This is part 3 of the onboarding floating point series. This series is intended to be used for onboarding of programmers new to the team to review a basic understanding of fixed-point and floating-point number formats, or for programmers who would like to remove some of the mystery from formats they may use everyday.
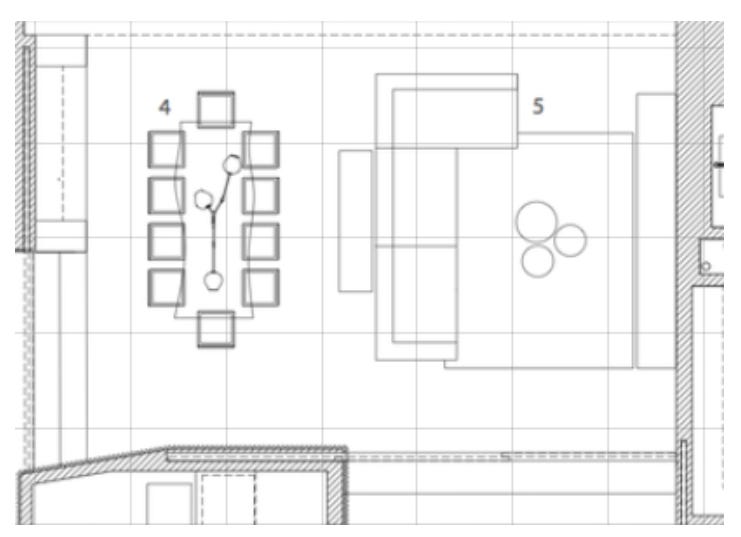
Let's say you’re making a game set in the interior of a house…
And you want to work with real-world sizes, so let’s put it on a 1-meter grid.
Looking at the size of our level, we could estimate that a range of about +/- 16 meters on each axis would work.
We also want to zoom in on areas, move players smoothly around the map, and handle detailed collisions.
We need to estimate the slowest expected movement and the expected simulation framerate. We might expect something to move slower than 1 meter per second, so we can estimate our lower speed bound to 1 centimeter per second. If we expect simulation to run at 60 frames per second, then we need to at least support a position resolution of 1/60 centimeters. Which we can round to 1mm.
Approximately what do we need?
Resolution: 1mm
Range: 32m
If we divide a meter into 1024 segments, that will give slightly better than the 1mm resolution we are looking for. Those 1024 values require 10 bits. If we are using 16 bits to store our value, that leaves 6 bits for whole number values, which gives a range of 64 meters. More than enough for what we need.
Fixed-point is a storage format for exact fractions of linear coordinate steps divided by a fixed number of segments. The resolution of the fractional part and the range of the integer part is completely dependent on context. There is no one format that can serve all purposes. As with all things, efforts to over-generalize a solution result in poor fit for all problems. We might for instance want to make a scifi space travel game where light-years are a more useful measure than millimeters.
Storage is generally either in a sign-magnitude form with a sign part, an integer part, and a fractional part, or in a two’s-complement signed-integer form.
Storage size usually mirrors hardware integer sizes available on the architecture being used (8 bit, 16 bit, 32 bit, 64 bit). Although it is not always the case. For instance, it might be useful to fit three 21 bit fixed-point values into one 64 bit integer as 3D coordinate vector.
To define a fixed-point storage format, answer the following questions:
How many maximum total bits are desired?
What fractional resolution is required?
How will signed values be handled?
For example, given the example above, we might answer:
Target 16 bits storage
10 bits of fractional resolution (0-1023)
Sign-magnitude
From that, you can derive the positive integer range of 5 bits (0-31). Conventionally, in sign-magnitude form this would be called 1:5:10 fixed-point.
|-----------------------------------------------------------|
| fixed-point sign-magnitude 1:5:10 |
|--------|------------------|---|-------|-------------------|
| hex | bin | s | m | value as fraction |
|--------|------------------|---|-------|-------------------|
| 0x0000 | 0000000000000000 | 0 | 0 | ( 0 + 0/1024) |
| 0x0400 | 0000010000000000 | 0 | 1024 | ( 1 + 0/1024) |
| 0x8400 | 1000010000000000 | 1 | 1024 | -( 1 + 0/1024) |
| 0x0600 | 0000011000000000 | 0 | 1536 | ( 1 + 512/1024) |
| 0xffff | 1111111111111111 | 1 | 32767 | -(31 + 1023/1024) |
| 0x7fff | 0111111111111111 | 0 | 32767 | (31 + 1023/1024) |
|--------|------------------|---|-------|-------------------|
Table of fixed-point sign-magnitude 1:5:10
https://godbolt.org/z/K3W1zd6heEXERCISE 3-1: Pick a game you’re familiar with and estimate the necessary resolution and range needed for world position values.Next: Part 4
Fixed-point as compression - Any given fixed-point format can be considered a method of compressing another, higher resolution fixed-point format.