Floating-point as compression

A floating-point format can be considered a (generally lossy) approach to compressing a high-resolution fixed-point format.

This is part 5 of the onboarding floating point series. This series is intended to be used for onboarding of programmers new to the team to review a basic understanding of fixed-point and floating-point number formats, or for programmers who would like to remove some of the mystery from formats they may use everyday.

As we did in fixed-point as compression, let’s consider a table of values in 1:16:15 fixed-point

uint32_t values[] = 
{ 
	0x012763c0, 0x0135f328, 0x0071e438, 0x012b9f10, 
	0x00be5ea8, 0x0001007c, 0x00010098, 0x000101b3, 
	0x00147dc8, 0x00904d60, 0x0000ffd0, 0x0058b330, 
	0x00010149, 0x000101a0, 0x0001011c, 0x0000806a, 
	0x00010139, 0x000101e5, 0x01a7a068, 0x0001012e, 
	0x0001012f, 0x00fa2f00, 0x000080f5 
};

However, in this case let’s assume the values represent time in seconds, and that these values are for profiling and measuring execution times of various parts of the asset build system.

Previously we were able to compress position values to 1:5:10 fixed-point, but in this case our values range from around 1 to 850 which is too large to fit in 5 bits of range (+/- 31). And there’s no obviously unused part of the resolution.

But can we find a way to make it fit?

Lossy Compression

Time has a property we can exploit here. In the case of profiling data, the longer the time, the less resolution matters. For instances, the difference between 900.0 and 900.1 seconds is much less valuable to capture than the difference between 1.0 and 1.1 seconds.

We’ll continue to use 10 bits to store the fractional value. But we’ll use the top-most enabled bit to determine which 10 bits to capture:

Let’s clear out the bottom bits to simulate what would happen if we were able to store those 10 bits.

EXERCISE 5-1: Duplicate the table above given input values in 1:16:15 format.

Let’s have a look at a couple examples.

Example 1: For values of 1-2, we will use 10 bits fractional exactly as in fixed-point.

0: 0000000000000001:000000011110101
0: 0000000000000001:0000000111xxxxx
0: (0b10000000111 << 0) / 1024 (10 bits fractional)
0: 1031 / 1024
= 1 + (7 / 1024)

Example 2: For values of 512-1024, the 10 bits will represent 9 bits of integer value and only one bit of fractional value. So between 512-1024, we have a resolution of 1/2.

0:0000001001001110:110001111000000 
0:0000001001001110:1xxxxxxxxxxxxxx
0: (0b10010011101 << 9) / 1024 
0: (1181 << 9) / 1024
0: 604672 / 1024
= 590 + (512 / 1024) 

EXERCISE 5-2: Print simulated compressed values as a fraction.

We can express that with the following pattern to compress rational numbers between 1 and 65535.

Additionally, perhaps we are also measuring runtime performance where values are more likely to be in the range of microseconds and milliseconds than in multiple seconds. Let’s look at this sample:

uint32_t values[] = 
{
	0x00000000, 0x00003c78, 0x00000333, 0x000006cc, 
	0x00000001, 0x00001895, 0x00000001, 0x0000037a, 
	0x00000005, 0x00000000, 0x0000000c, 0x000009d5, 
	0x0000003e, 0x000000fb, 0x00000004, 0x000018c6,
	0x000000ff, 0x00000042, 0x00000263, 0x00000ba4, 
	0x000038d1, 0x00000e69, 0x00000039
};

|------------|--------|----------|
| from       | to     | approx.  |
|------------|--------|----------|
| 0x00000000 | 0x0000 | 0.000000 |
| 0x00003c78 | 0x378f | 0.472412 |
| 0x00000333 | 0x2533 | 0.020309 |
| 0x000006cc | 0x2acc | 0.053101 |
| 0x00000001 | 0x0000 | 0.000000 |
| 0x00001895 | 0x3225 | 0.192017 |
| 0x00000001 | 0x0000 | 0.000000 |
| 0x0000037a | 0x257a | 0.021393 |
| 0x00000005 | 0x0801 | 0.000122 |
| 0x00000000 | 0x0000 | 0.000000 |
| 0x0000000c | 0x0c04 | 0.000245 |
| 0x000009d5 | 0x2cea | 0.076782 |
| 0x0000003e | 0x141e | 0.001005 |
| 0x000000fb | 0x1c7b | 0.004375 |
| 0x00000004 | 0x0800 | 0.000122 |
| 0x000018c6 | 0x3231 | 0.193481 |
| 0x000000ff | 0x1c7f | 0.004391 |
| 0x00000042 | 0x1802 | 0.001957 |
| 0x00000263 | 0x2463 | 0.017136 |
| 0x00000ba4 | 0x2dd2 | 0.090942 |
| 0x000038d1 | 0x371a | 0.443848 |
| 0x00000e69 | 0x2f34 | 0.112549 |
| 0x00000039 | 0x1419 | 0.001000 |
|------------|--------|----------|

What do we do with numbers between 0 and 1?

We can just continue the pattern above. Note that now we need to right-shift the fractional value instead of left-shifting. When less than 10 fractional bits are stored, they will be stored in the low bits (in other words, packed to the right.)

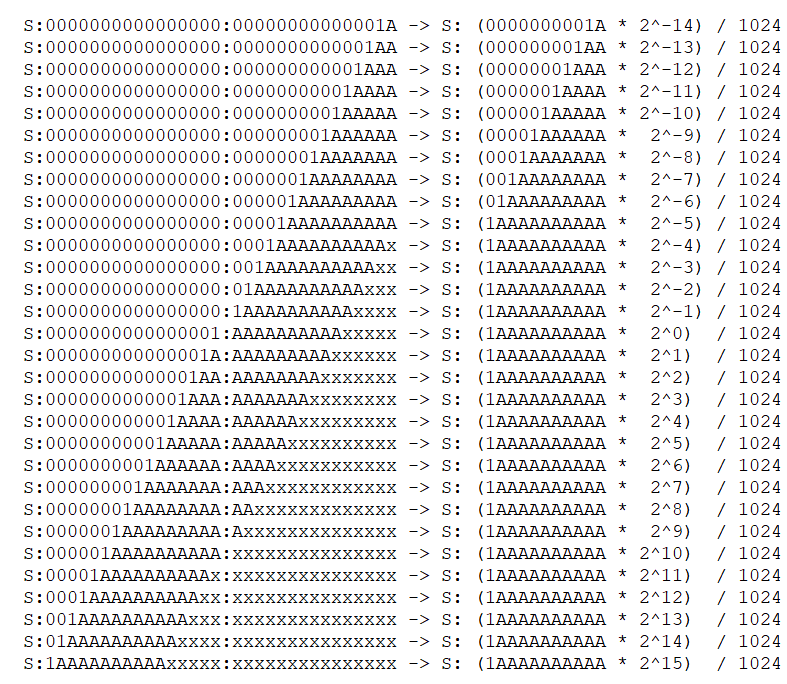
A more complete full pattern becomes:

EXERCISE 5-3: Modify code from EXERCISE 5-1 and EXERCISE 5-2 using the full pattern above.

Which we can also express the shifts in terms of multiply with power of two.

What do we need to store at this point?

• 1 bit sign

• Exponent (shift amount) between -14 and 15.

• Fractional part (mantissa) 10 bits

We can store exponent as offset-15 (values 1-30) which will fit nicely in 5 bits.

If exponent value is zero, the rational value will be (mantissa * 2^-14)/1024. i.e. without a leading one bit. These are called as sub-normal values.

This would be conventionally called s10e5 floating-point format.

The compression routine from 1:16:15 fixed-point might look something like this:

uint16_t compress( uint32_t d )
{
  int s   = d >> 31;
  int clz = __builtin_clz(d&0x7fffffff)-1;
  int exp = (30-clz);
  int sa  = exp-15;

  // no sub-normal values from 1:16:15 format
  if ( clz > 29 )
  {
    exp = 0;
    sa  = 0;
  }

  uint32_t d10 = d >> 5; // align to 10 bit fraction
  uint32_t fraction = d10 & 0x3ff;
  if (sa > 0)
  {
    fraction = (d10 >> sa) & 0x3ff;
  }
  else if (sa < 0)
  {
    if (sa >= -4)
    {
      fraction = (d >> (5+sa)) & 0x3ff;
    }
    else
    {
      fraction = d & (0x3ff >> -(sa+5));
    }
  }
  return (s<<15) | (exp << 10) | fraction;
}

And if we apply to our test values, we get:

EXERCISE 5-4: Write an uncompress() function which converts s5e10 floating-point values to 1:16:15 fixed-point.

uint16_t test_values[] =  {  0x609d, 0x60d7, 0x5b1e, 0x60ae, 
                             0x5df2, 0x4001, 0x4002, 0x4006, 
                             0x511f, 0x5c82, 0x3ffe, 0x598b, 
                             0x4005, 0x4006, 0x4004, 0x3c03, 
                             0x4004, 0x4007, 0x629e, 0x4004, 
                             0x4004, 0x5fd1, 0x3c07, 0x0000, 
                             0x378f, 0x2533, 0x2acc, 0x0000, 
                             0x3225, 0x0000, 0x257a, 0x0801, 
                             0x0000, 0x0c04, 0x2cea, 0x141e, 
                             0x1c7b, 0x0800, 0x3231, 0x1c7f, 
                             0x1802, 0x2463, 0x2dd2, 0x371a, 
                             0x2f34, 0x1419 };

EXERCISE 5-5: 

Given input data in 1:8:10 (19 bits) fixed point:

|-------|--------------|--------------------------|
| Sign  | Integer      | Fractional               | 
|-------|--------------|--------------------------|
| 1 bit | 8 bits       | 10 bits                  |
|-------|--------------|--------------------------|

And the following pattern to compress values to 8 bits:

  |-----------------------|------------|
  | 1:8:10                | 1:4:3      |
  |-----------------------|------------|
  | s:1abcxxxx:xxxxxxxxxx | s:1111:abc |
  | s:01abcxxx:xxxxxxxxxx | s:1110:abc |
  | s:001abcxx:xxxxxxxxxx | s:1101:abc |
  | s:0001abcx:xxxxxxxxxx | s:1100:abc |
  | s:00001abc:xxxxxxxxxx | s:1011:abc |
  | s:000001ab:cxxxxxxxxx | s:1010:abc |
  | s:0000001a:bcxxxxxxxx | s:1001:abc |
  | s:00000001:abcxxxxxxx | s:1000:abc |
  | s:00000000:1abcxxxxxx | s:0111:abc |
  | s:00000000:01abcxxxxx | s:0110:abc |
  | s:00000000:001abcxxxx | s:0101:abc |
  | s:00000000:0001abcxxx | s:0100:abc |
  | s:00000000:00001abcxx | s:0011:abc |
  | s:00000000:000001abcx | s:0010:abc |
  | s:00000000:0000001abc | s:0001:abc |
  | s:00000000:0000000abc | s:0000:abc |
  |-----------------------|------------|

Compressed format is s3e4 floating-point:

|-------|------------------|---------------|
| sign  | exponent         | mantissa      | 
|-------|------------------|---------------|
| 1 bit | 4 bits           | 3 bits        |
|-------|------------------|---------------|

Write functions to compress() and uncompress().

REFERENCE: Check out the G.711 audio codec as a concrete example of approaching floating point as a compression format. 

Next: Part 6

Floating-point as fractions - Like fixed-point, floating-point is a format which stores rational numbers as fractions.