Floating-point Multiplication

Floating-point values are fractions. Multiplying floating-point numbers is multiplying fractions.

This is part 10 of the onboarding floating point series. This series is intended to be used for onboarding of programmers new to the team to review a basic understanding of fixed-point and floating-point number formats, or for programmers who would like to remove some of the mystery from formats they may use everyday.

We’ll continue using the s10e5 floating-point format from floating point as fractions.

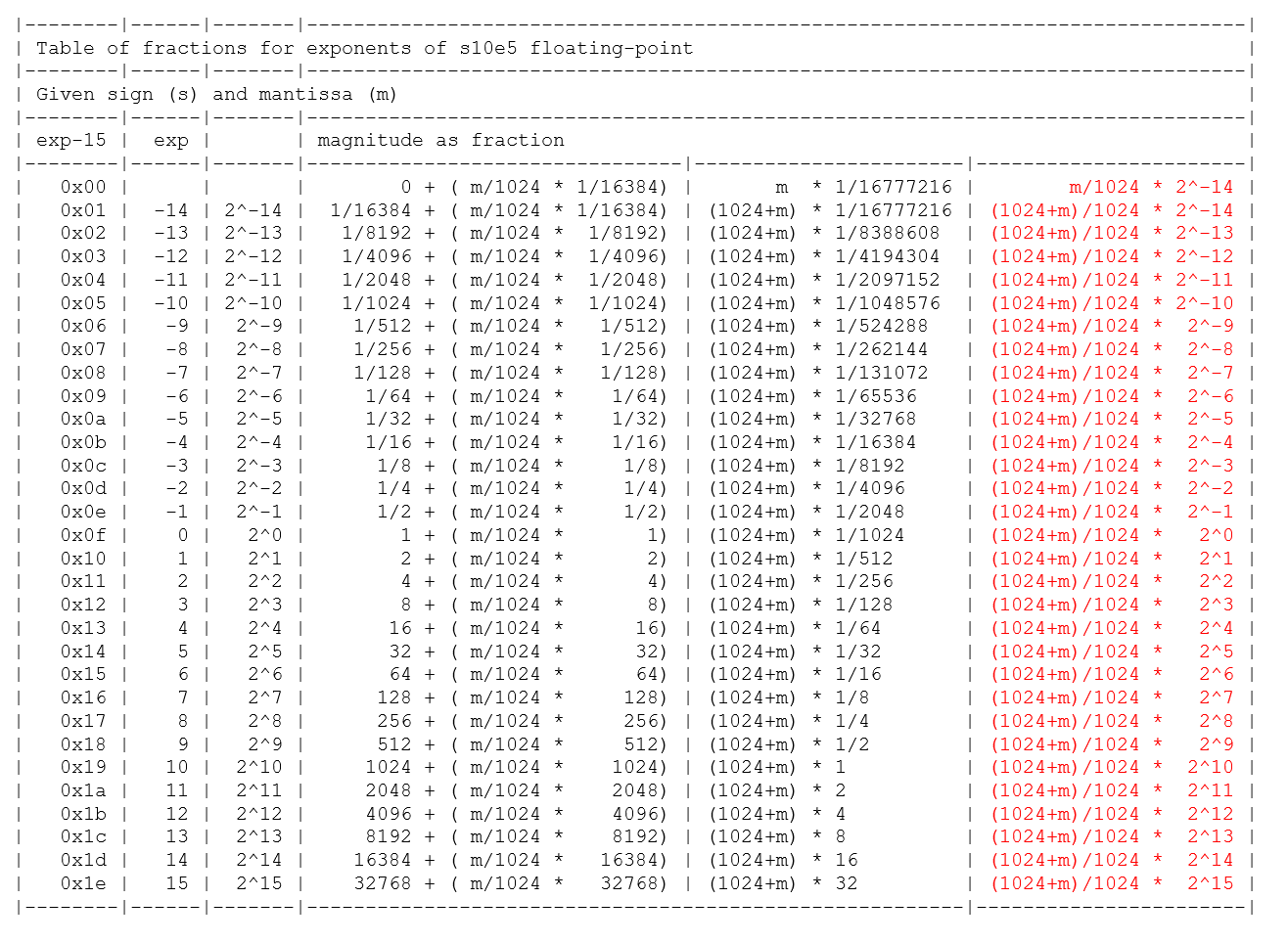
We can express s10e5 as a fraction:

\(s \cdot \left( 2^{x} + \frac{2^{x}m}{1024} \right)\)

Except where exp15 is zero:

\(s \cdot \left( \frac{2^{-14}m}{1024} \right)\)

TERMS
-----------------------------------------------------------------------------
| sign  | x15                 | m                                           |
|-------|---------------------|---------------------------------------------|
| 1 bit | 5 bits              | 10 bits                                     |
-----------------------------------------------------------------------------
| sign        | 1 bit value exactly as stored (1=negative, 0=positive)      |
| x15         | 5 bit value exactly as stored as offset-15                  |
| m           | 10 bit value exactly as stored as unsigned integer          |
| x           | exponent as signed integer                                  |
| s           | sign as signed integer (-1=negative, 1=positive)            |
| magnitude   | unsigned value as f(x15,m)                                  |

Multiplication

If we rearrange the fractions, we can define s10e5 floating-point as:

\( s \cdot \left(\frac{1024+m}{1024}\right) \cdot 2^{x}\)

Except for where exp-15 is zero:

\(s \cdot \left(\frac{m}{1024}\right) \cdot 2^{-14}\)

Multiplying two values (c = a*b):

\(\left(s_a \cdot \frac{1024+m_a}{1024} \cdot 2^{x_a}\right)\cdot\left(s_b \cdot \frac{1024+m_b}{1024} \cdot 2^{x_b}\right) \)

\(\left(s_a \cdot s_b\right) \left( \frac{1024+m_a}{1024} \cdot \frac{1024+m_b}{1024} \right) \left( 2^{x_a} \cdot 2^{x_b} \right) \)

\(\left(s_a \cdot s_b\right) \left( \frac {\left(1024+m_a\right)\left(1024+m_b\right)} {1024 \cdot 1024} \right) 2^{x_a + x_b}\)

And if we replace:

\(s_{c} = s_{a} \cdot s_{b}\)

\(x_{c} = x_{a} + x_{b}\)

\(significand_{c} = \frac {\left(1024+m_a\right)\left(1024+m_b\right)} {1024 }\)

We can re-write the result as:

\(s_{c} \cdot \frac { significand_{c} } { 1024 } \cdot 2^{x_{c}}\)

We can extract the mantissa as with addition. And like addition, at this point the fraction may need to be normalized if significand_c is too large or too small for mantissa to fit in 10 bits unsigned.

\(m_{c} = significand_{c}-1024\)

Which gives us the result in the correct form:

\(s_{c} \cdot \frac { 1024 + m_{c} } { 1024 }\)

Except in the case where x15 is zero:

\(m = significand_{c}\)

\(s_{c} \cdot \frac { m_{c} } { 1024 }\)

Then normalize.

uint32_t 
mul(uint16_t a, uint16_t b)
{
  //
  // Extract components of a,b where:
  //   s     = negative=-1, positive=0
  //   m     = 10 bit unsigned mantissa
  //   x15   = 5 bit exponent in offset-15
  //   x15nz = (x15 != 0)?-1:0
  //   x     = if (x15 == 0) -14
  //           else x15 as two's-complement 
  //

  uint16_t a_s     = (int16_t)a >> 15; 
  uint16_t a_m     = a & 0x03ff;
  uint16_t a_x15   = (a & 0x7c00) >>  10;
  uint16_t a_x15nz = (int16_t)(-a_x15)>>15;
  int16_t  a_x     = (a_x15nz & (a_x15-15)) | ((~a_x15nz) & -14);

  uint16_t b_s     = (int16_t)b >> 15; 
  uint16_t b_m     = b & 0x03ff;
  uint16_t b_x15   = (b & 0x7c00) >>  10;
  uint16_t b_x15nz = (int16_t)(-b_x15)>>15;
  int16_t  b_x     = (b_x15nz & (b_x15-15)) | ((~b_x15nz) & -14);

  //
  // Create significand of a,b where:
  //  if (x15 != 0) significand = 1024 + m
  //  else          significand = m
  //

  uint16_t a_significand = a_m + (a_x15nz&1024);
  uint16_t b_significand = b_m + (b_x15nz&1024);
 
  // 
  // Multiply
  //   - 10 bit fixed-point multiply significands as (a*b)>>10
  //   - sign(a) * sign(b)
  //   - half round up
  //   - defer shift-right 10 bits until normalization
  //     in case left-shift is needed, so we don't lose
  //     the values.
  //

  uint16_t c_s             = a_s ^ b_s;
  uint32_t c_significand   = a_significand * b_significand;
  int16_t  c_x             = a_x + b_x;

  //
  // Normalize
  //

  // clz(c_significand) = (0,32)
  uint32_t signz    = (int32_t)(-c_significand) >> 31;
  int16_t  sigclz31 = __builtin_clz( c_significand );
  int16_t  sigclz   = (signz & sigclz31)|((~signz)&32);

  // reduce by exponent until 10 bits of mantissa 
  int16_t  hi_sa            = sigclz-11;
  int16_t  norm_x           = c_x - hi_sa;
  uint16_t norm_x_underflow = (norm_x+14) >> 15;
  uint16_t norm_x15         = ((~norm_x_underflow) & (norm_x+15));
  int16_t  norm_sa          = ((~norm_x_underflow) & (hi_sa-10))
                            | (norm_x_underflow & (c_x+4));

  // if norm_sa < 0, then right shift, else left shift.
  uint16_t norm_sa_sign     = norm_sa >> 15;
  int16_t  norm_rsa         = norm_sa_sign & (-norm_sa);
  int16_t  norm_lsa         = (~norm_sa_sign) & norm_sa;
  uint16_t norm_significand = (c_significand << norm_lsa) >> norm_rsa;

  //
  // Store
  //

  uint16_t c_m = norm_significand & 0x3ff;
  uint16_t c   = (c_s << 15) | (norm_x15 << 10) | c_m;

  return c;
}

Exercise 10-1: Create a version of mul() for s23e8 floating-point. Compare results to using float instructions.

REFERENCE: See Berkely SoftFloat [github.com/ucb-bar] for implementations of common operations for different floating-point formats.

Normalization as compression

The multiplication of significands is a 10 bit fixed-point multiply. Consider the result as a 20 bit value. As covered in floating-point as compression, you can also think of the normalization process as a pattern to compress that 20 bit result into a 10 bit mantissa and change to the exponent.

| significand (20 bit)  |  m         | change to x |
|-----------------------|------------|-------------|
| 1AAAAAAAAAAxxxxxxxxx  | AAAAAAAAAA | x+9         |
| 01AAAAAAAAAAxxxxxxxx  | AAAAAAAAAA | x+8         |
| 001AAAAAAAAAAxxxxxxx  | AAAAAAAAAA | x+7         |
| 0001AAAAAAAAAAxxxxxx  | AAAAAAAAAA | x+6         |
| 00001AAAAAAAAAAxxxxx  | AAAAAAAAAA | x+5         |
| 000001AAAAAAAAAAxxxx  | AAAAAAAAAA | x+4         |
| 0000001AAAAAAAAAAxxx  | AAAAAAAAAA | x+3         |
| 00000001AAAAAAAAAAxx  | AAAAAAAAAA | x+2         |
| 000000001AAAAAAAAAAx  | AAAAAAAAAA | x+1         |
| 0000000001AAAAAAAAAA  | AAAAAAAAAA | x           |
| 00000000001AAAAAAAAA  | AAAAAAAAA0 | x-1         |
| 000000000001AAAAAAAA  | AAAAAAAA00 | x-2         |
| 0000000000001AAAAAAA  | AAAAAAA000 | x-3         |
| 00000000000001AAAAAA  | AAAAAA0000 | x-4         |
| 000000000000001AAAAA  | AAAAA00000 | x-5         |
| 0000000000000001AAAA  | AAAA000000 | x-6         |
| 00000000000000001AAA  | AAA0000000 | x-7         |
| 000000000000000001AA  | AA00000000 | x-8         |
| 0000000000000000001A  | A000000000 | x-9         |

Conversion to float

For a comparison with outputs of compiler-generated float conversions, see:
https://godbolt.org/z/E4aderGfG

Next: Part 11

Floating-point Division - Floating-point values are fractions. Dividing floating-point numbers is dividing fractions.